Enhancing Security and Privacy in Federated Learning using Low-Dimensional Update Representation and Proximity-Based Defense

Background

Federated Learning (FL) enables collaborative model training across decentralized clients while preserving data locality, with updates aggregated by a server. While FL achieves accuracy comparable to centralized methods, its trustworthiness hinges on both clients and servers. Malicious clients controled by Byzantine adversary can poison local updates to manipulate the global model. Classic aggregation rules (e.g., FedAvg) lack robustness against such threats. Simultaneously, servers pose privacy risks via reconstruction attacks (e.g., DLG, InvertGrad) that infer sensitive data from plaintext updates.

Existing defenses inadequately address the interplay between Byzantine robustness and privacy.

Motivation

Current SMPC-based privacy solutions incur prohibitive computational costs when applied to high-dimensional model updates. For instance, pairwise squared Euclidean distance (SED) calculations for Byzantine detection scale quadratically with model size, rendering SMPC impractical. Additionally, adversaries increasingly employ sophisticated poisoning strategies, such as aligning poisoned updates with benign statistical properties (e.g., matching element-wise mean/variance), evading traditional detection.

These gaps necessitate a lightweight, privacy-preserving detection method to distinguish poisoned updates without compromising efficiency or security.

Method under plaintext model updates

FLURP operates in three phases.

1. Each client $i$ compute LUR via LinfSample: sliding windows extract $l_{\infty}$norms from model update, compressing high-dimensional vectors into low-dimensional representations. This preserves discriminative features for poisoning detection while reducing SMPC overhead.
2. The servers construct a SED matrix using LURs.
3. Given $m$ participating clients, at the beginning of each global round, each client’s neighbor count is initialized to $0$. The server computes the $\lfloor\frac{m}{2}\rfloor$ closest clients for each client $i$, and increments their neighbor counts by $1$. Subsequently, clients with neighbor counts of at least $\lfloor\frac{m}{2}\rfloor$ are classified as benign, and their updates are aggregated using weighted averaging to form the global update.

Method under model updates in form of secret sharing

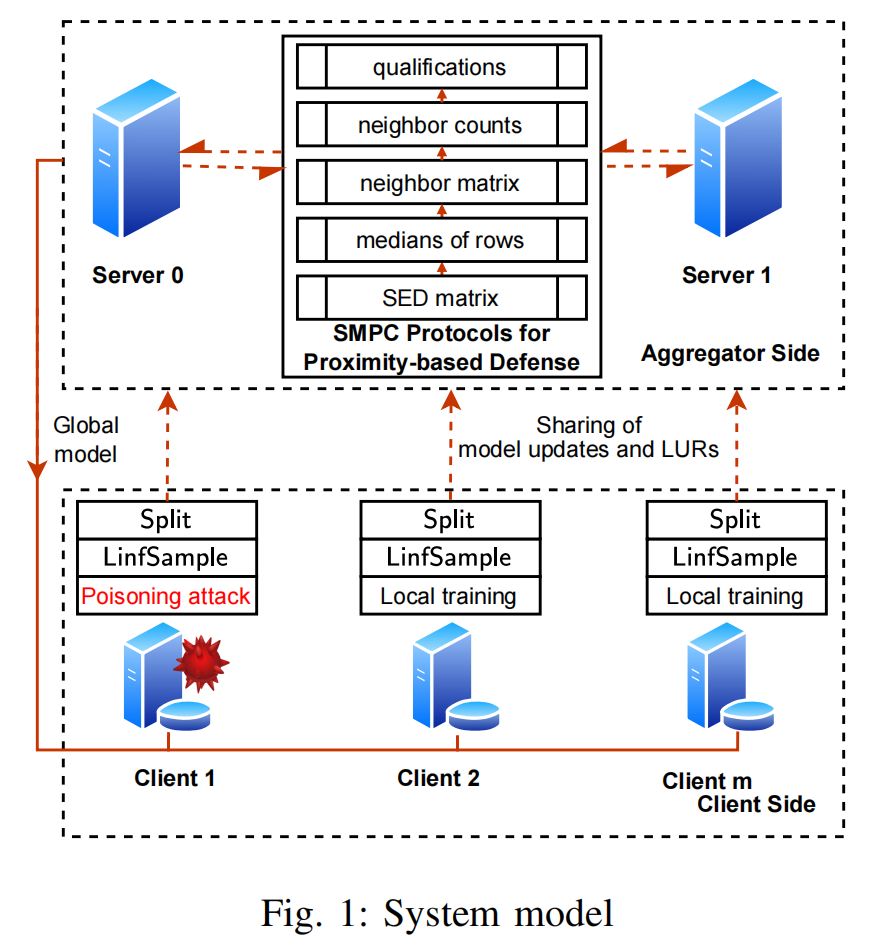
On the client side, after local training, each client $i$ applies $\mathsf{LinfSample}$ to their update $\boldsymbol{g}_i$, yielding the local update representation (LUR) $\boldsymbol{v}_i$. Subsequently, both $\boldsymbol{g}_i$ and $\boldsymbol{v}_i$ are split into Arithmetic sharing and transmitted to the servers.

On the aggregator side, the servers execute a series of SMPC protocols to implement a privacy-preserving proximity-based defense. They compute secret shares of the following:

1. the SED matrix of LURs,
2. the median of each row in the SED matrix
3. the neighbor matrix,
4. neighbor counts for all clients
5. qualifications of all clients, which determine which clients can contribute to the global model.

Details of SMPC protocols on servers

To prevent the leakage of neighborhood relationships among clients due to the revelation of comparison results during the quick select process, the servers invoke $\mathsf{matrixSharedShuffle}$ to independently shuffle all rows of $\langle \boldsymbol{M} \rangle$ and produce $\langle \tilde{\boldsymbol{M}} \rangle$. The servers then use $\mathsf{mulRowQuickSelect}$ to compute shares of the medians for all rows, denoted $\lbrace \langle \mu_i \rangle \rbrace_{i \in [1,m]}$.

Recall that, half of $m$ clients closest to client $i$ are regarded as $i$’s neighborhood. That is, for any two clients $i, j \in [1, m]$, if $\langle {M}{i,j} \rangle < \langle \mu{i} \rangle$, client $j$ is a neighbor of client $i$, resulting in $\langle {N}_{i,j} \rangle = 1$ in the neighbor matrix $\langle \boldsymbol{N} \rangle$.

The servers compute the sum of the $i$-th column of $\langle \boldsymbol{N} \rangle$ as the neighbor count $\langle s_i \rangle$ received by client $i$.

The servers compare the shares of $m$ pairs of neighbor counts and thresholds, where $\langle q_i \rangle^B = 1$ indicates that the neighbor count $s_i$ is greater than $\lfloor \frac{m}{2} \rfloor - 1$. In this case, $\boldsymbol{g}_i$ is considered benign and qualifies for aggregation in the current round.

Finally, the servers reveal $\langle q_i \rangle^B$ and aggregate the updates of the clients based on weights, resulting in a global update used to update the global model and proceed with the next round of global iteration.

It is noteworthy that the global updates, obtained through splitting, aggregating, and revealing local model updates, exhibit virtually no impact on precision. The FLURP framework utilizes carefully designed secure and efficient SMPC protocols to enable servers to shuffle, anonymize, and collectively determine on the most reliable updates through a robust proximity-based defense. It also effectively diminishes the impact of potentially poisoned updates by ensuring that only those endorsed by a majority are considered.

Details of SMPC protocols

Please refer to the paper.

Experiments

Tasks

• Train and test on CIFAR-10 (50k train, 10k test, 10 classes, 32x32 color images) using ResNet10 (4.9M params).
• Train and test on ImageNet-12 (12.5k train, 3.1k test, 12 classes, 224x224 color images) using MobileNet-V2 (2.2M params).
• Evaluate AgNews (120k train, 7.6k test, 4 categories) using Bi-LSTM (4.6M params, BERT tokenizer, 128-dim embeddings, 256 hidden units).

  Comparison of Sampling Methods

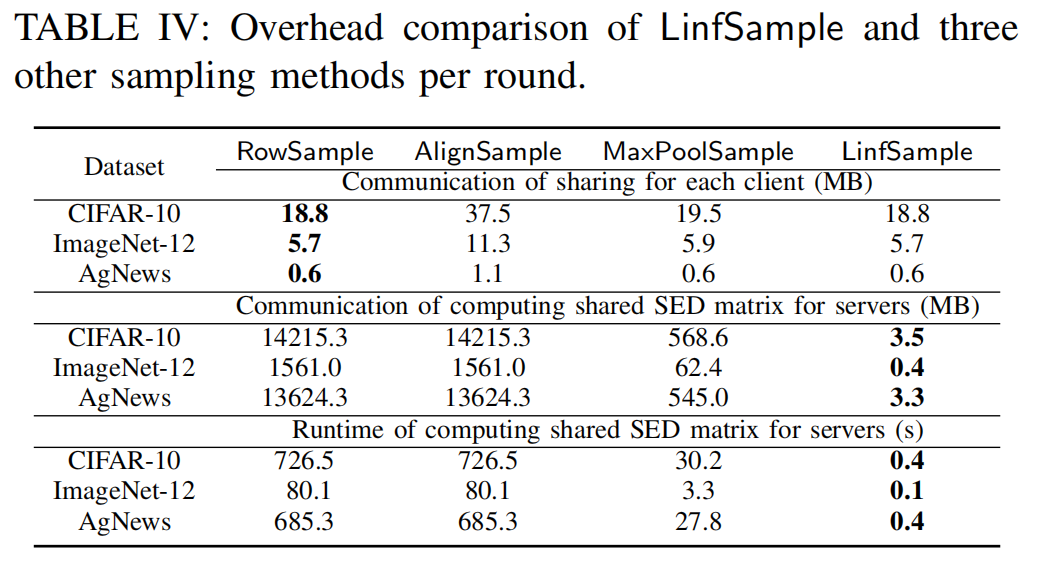
  To demonstrate the superior resistance of $\mathsf{LinfSample}$ against Byzantine attacks and its ability to reduce SMPC overhead in computing the shared SED matrix, we apply the same proximity-based defense to evaluate four different sampling methods.

• Byzantine resilience

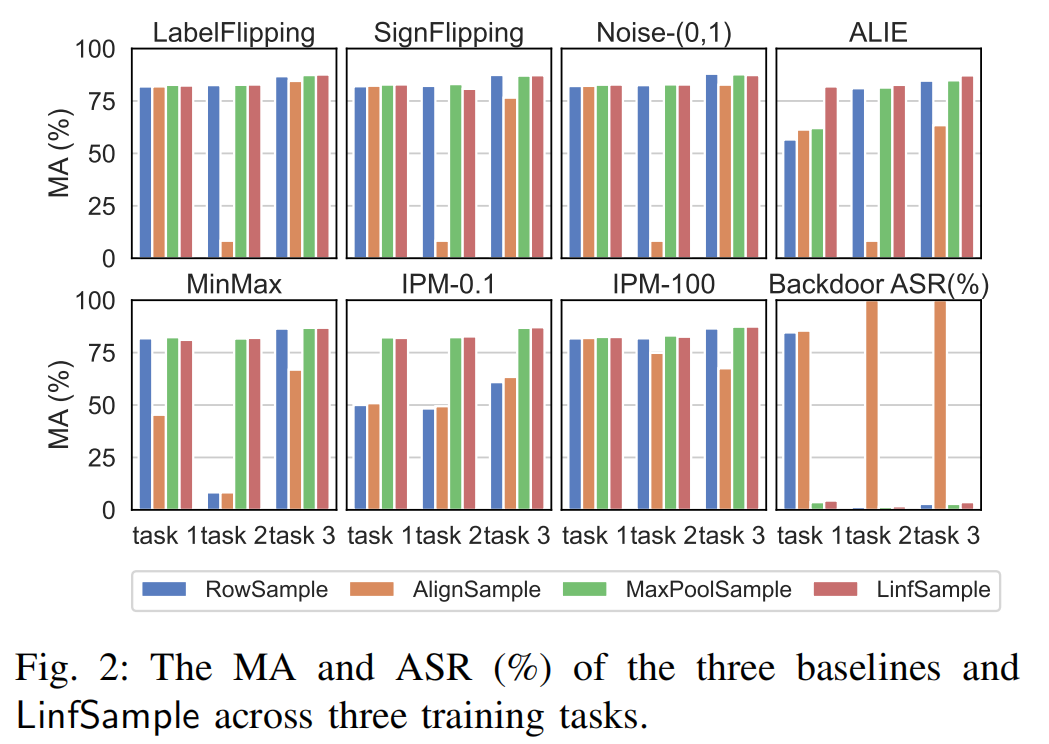
• Communication of client uploads for Sharing
• Overhead of computing shared SED matrix

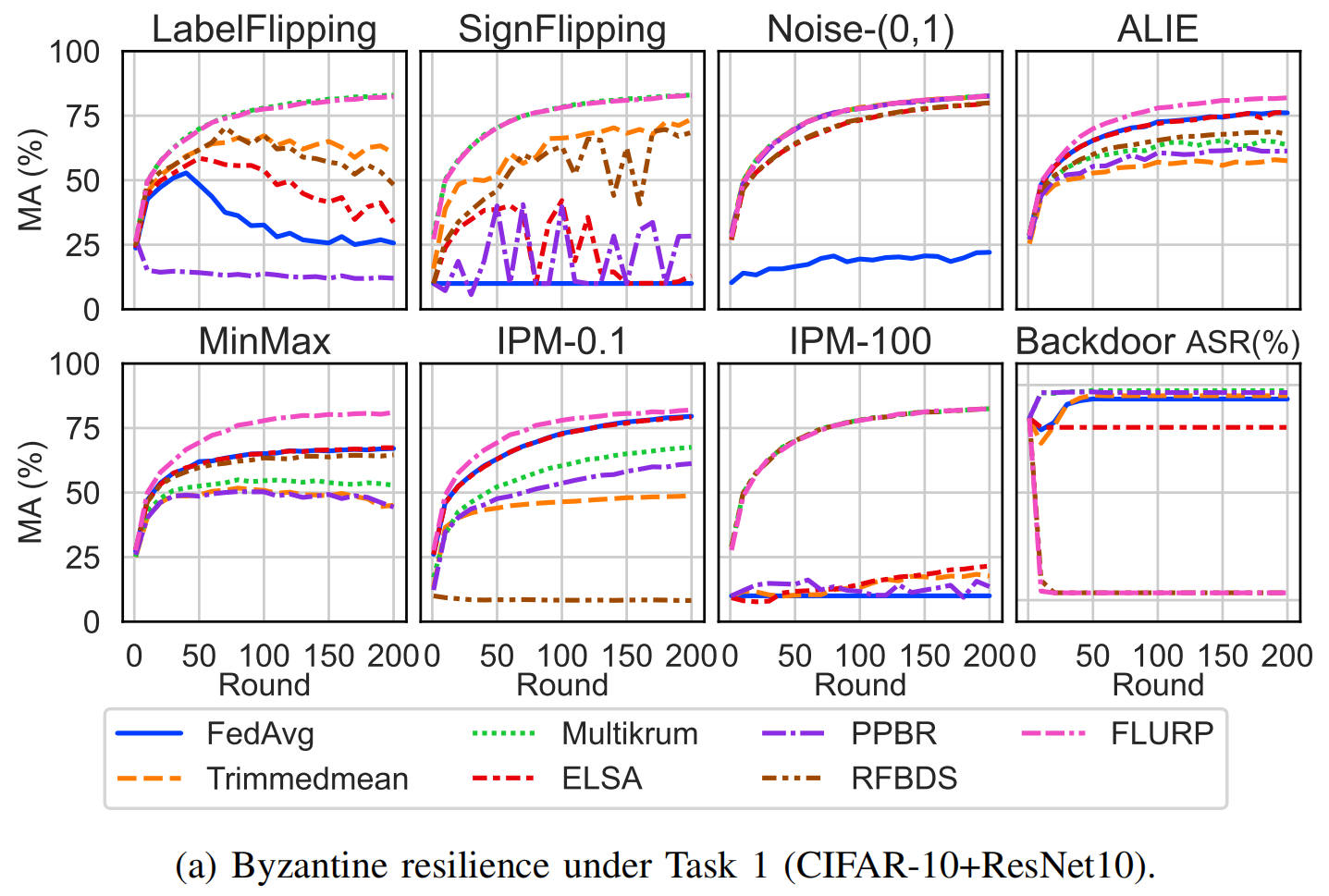
Byzantine Robustness of FLURP

We evaluate the Byzantine resilience of six baselines and FLURP. Notably, FLURP is the only method that effectively resists Backdoor attacks across all tasks.

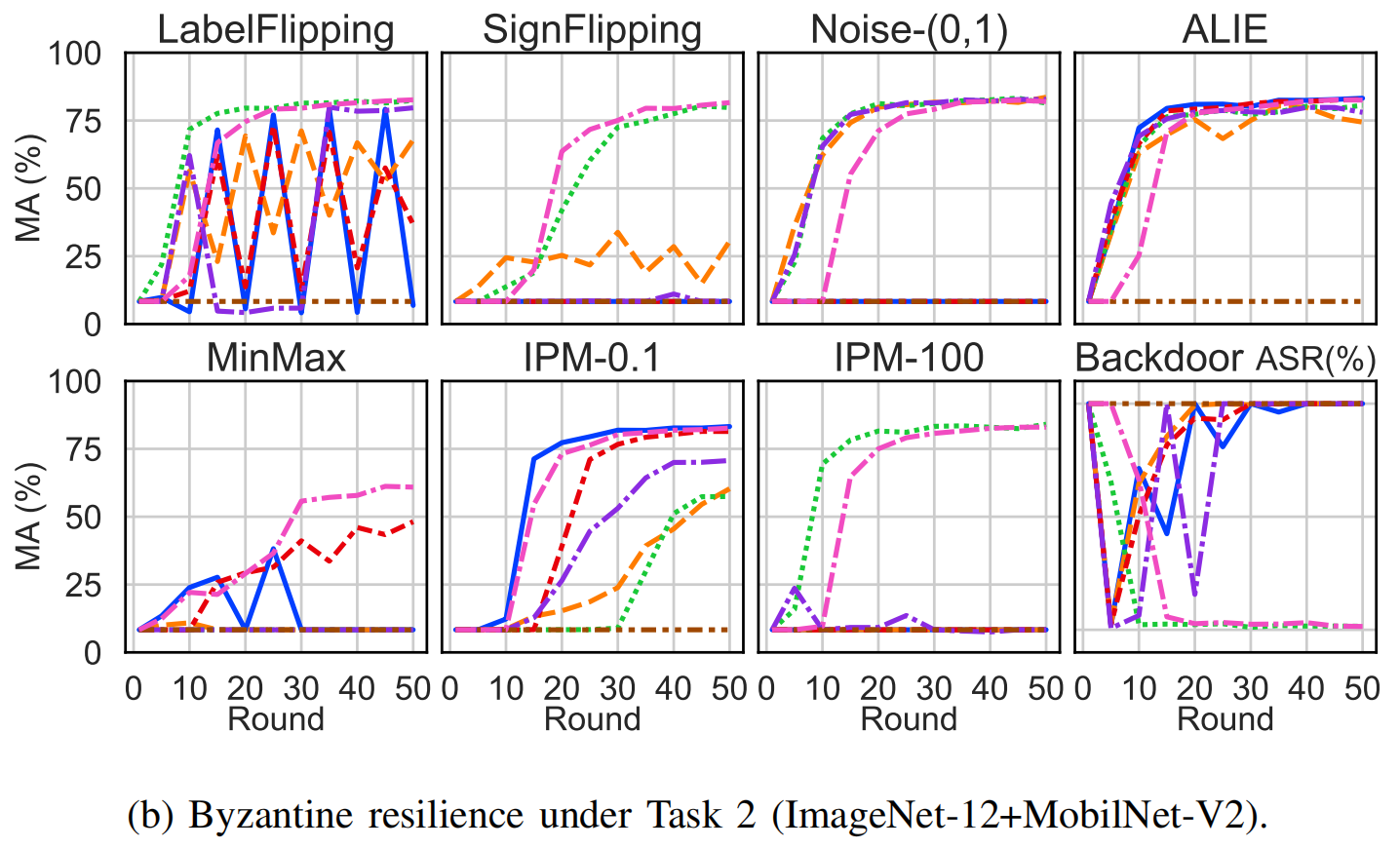
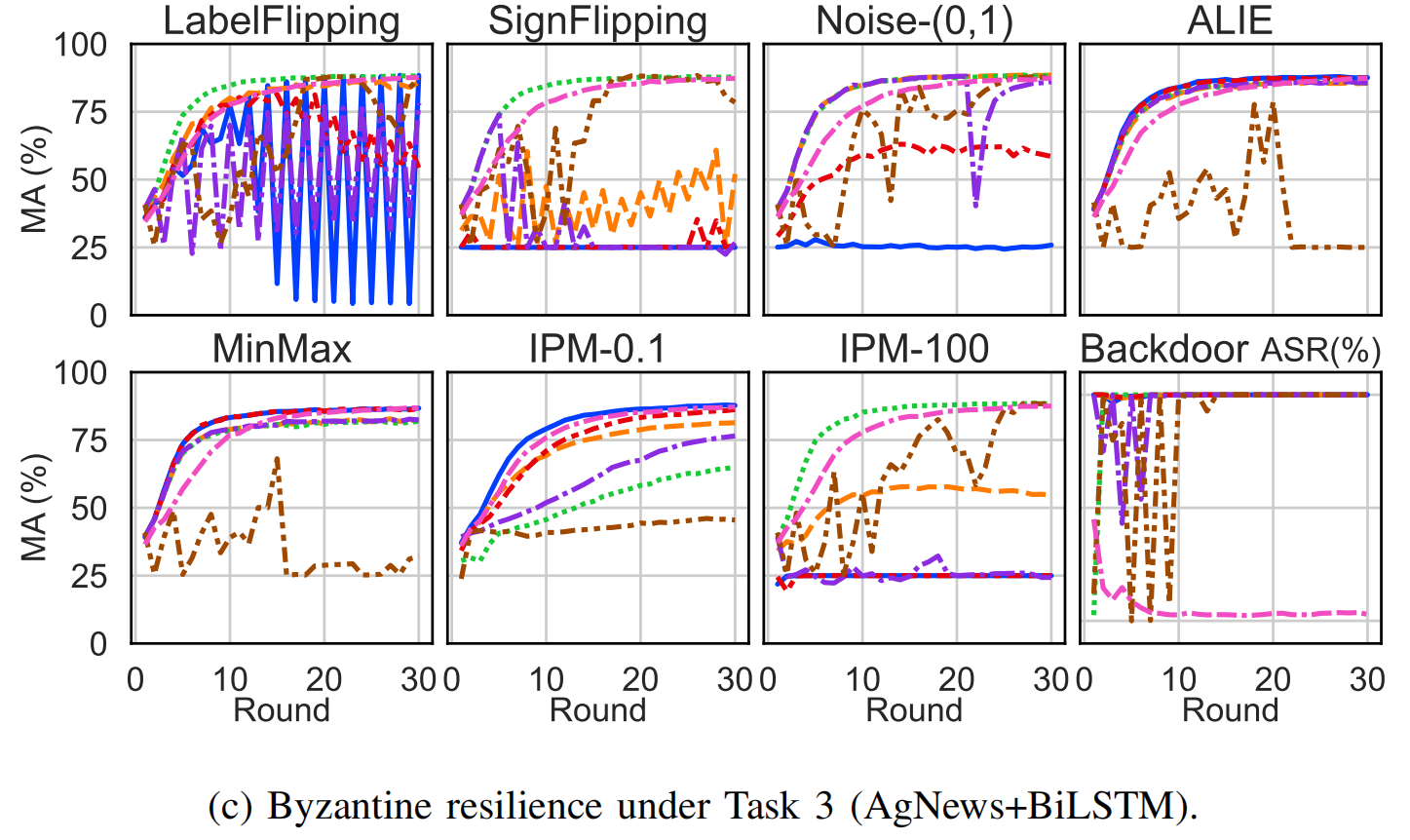
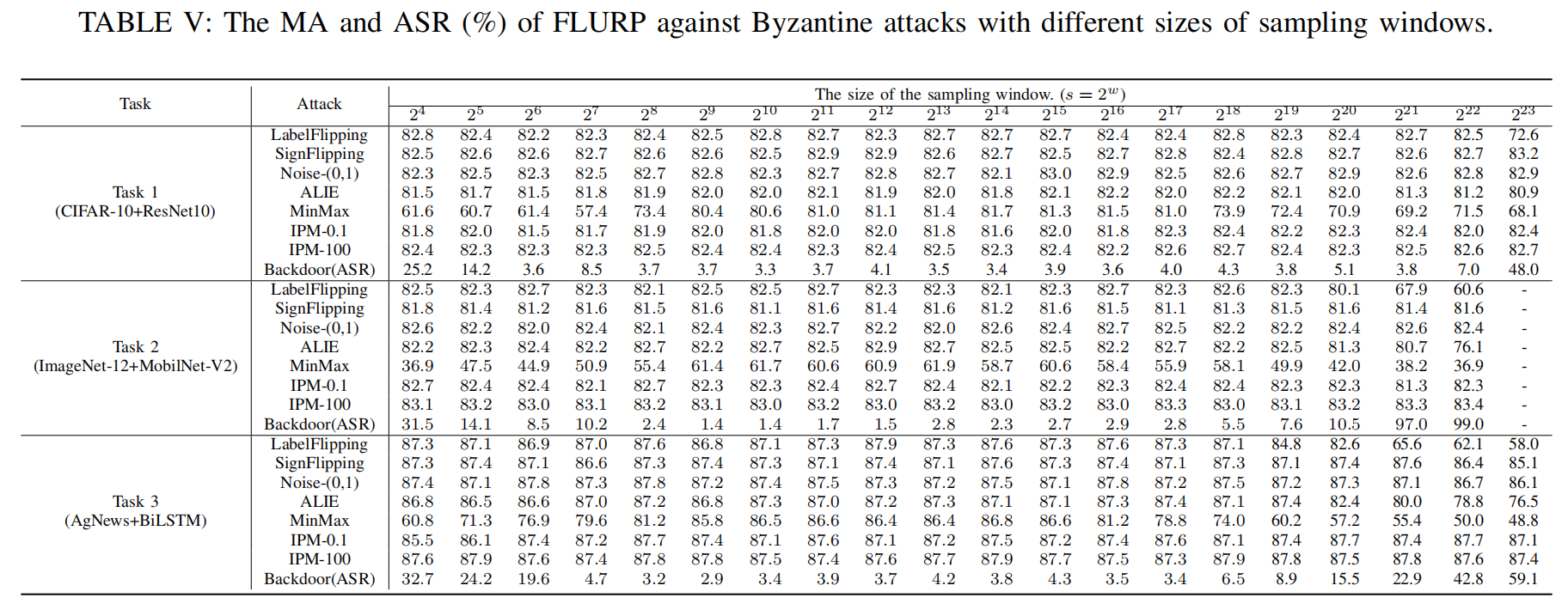
Influence of Window Size

Based on empirical analysis of the experimental results, a window size of $2^{11}$, $2^{12}$, $2^{13}$, or $2^{14}$ is deemed optimal for these million-sized models, striking the best balance between overhead and defense.

Impact of Client Data Distribution

FLURP remains a strong contender, especially when $\alpha$ is high. As $\alpha$ decreases, filtering out malicious clients becomes harder, but FLURP still provides robust defense in most situations.

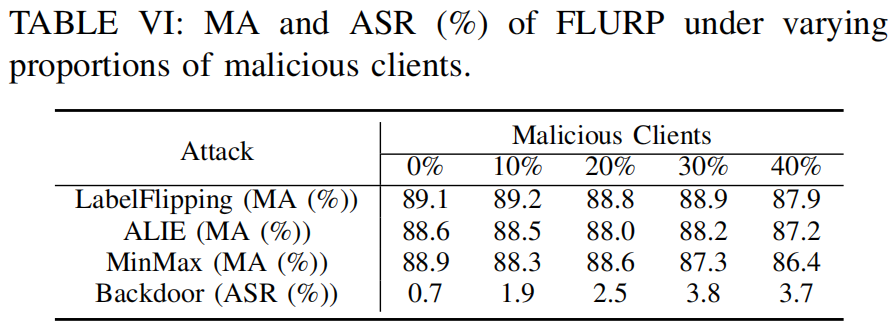
Impact of the Proportion of Malicious Clients

FLURP effectively mitigates the impact of backdoor attacks, even with a higher proportion of malicious clients, making it a highly effective defense for FL systems.

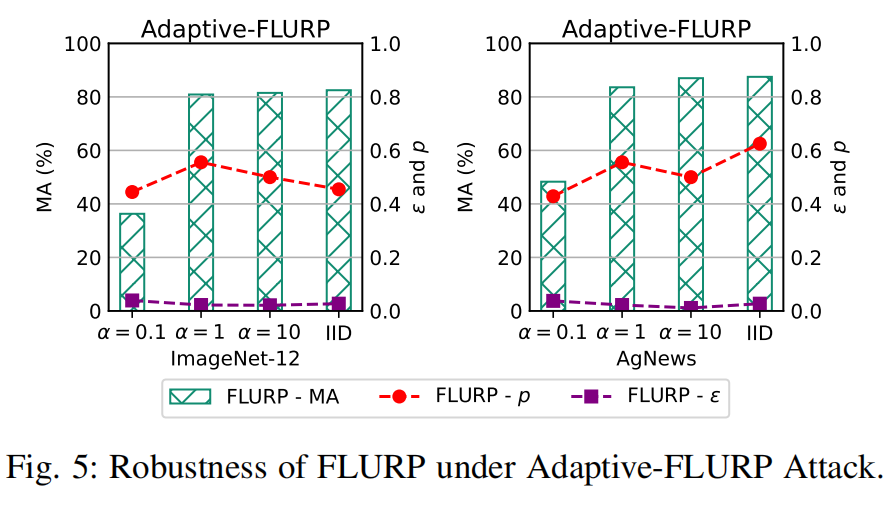
Adaptive Attack against FLURP

FLURP effectively mitigates Adaptive-FLURP attacks by forcing adversaries to use smaller scaling factors ($\gamma$) to evade detection, resulting in minimal global model deviation and negligible impact on model accuracy (MA). Even under non-IID distributions and increased benign update distances, FLURP maintains robust model performance, demonstrating its reliability against adaptive adversaries.

Conclusion

The FLURP framework enhances data security, privacy, and access control in distributed environments by integrating LURs and a privacy-preserving proximity-based defense, effectively countering Byzantine adversaries. It reduces SMPC computational and communication overhead, improving FL robustness and ensuring safer AI data management.

Future work will focus on optimizing FLURP for complex non-IID distributions and defending against LUR-forging adversaries by transforming $\mathsf{LinfSample}$ into a two-server SMPC protocol.

Citation

@ARTICLE{10878290,
  author={Li, Wenjie and Fan, Kai and Zhang, Jingyuan and Li, Hui and Lim, Wei Yang Bryan and Yang, Qiang},
  journal={IEEE Transactions on Knowledge and Data Engineering}, 
  title={Enhancing Security and Privacy in Federated Learning using Low-Dimensional Update Representation and Proximity-Based Defense}, 
  year={2025},
  volume={},
  number={},
  pages={1-14},
  doi={10.1109/TKDE.2025.3539717}}